1. Алгебра
  2. При каком значении переменной

При каком значении переменной x многочлен x^2+8x+12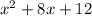x^2+8x+12 принимает наименьшее значение?

Если ответ получился нецелым, запишите его в виде обыкновенной несократимой дроби, не выделяя целую часть.

Например, 37/10, 2/3

ladomix ladomix    3   28.10.2020 16:41    3

Ответы
rahim55 rahim55  27.11.2020 16:42

Пускай данный многочлен представляет функцию f(x):

f(x) = {x}^{2} + 8x + 12

Данная функция – парабола, ветви которой направлены вверх, поэтому минимальное значение исходного многочлена будет равняться минимальному значению функции f(x), то есть её вершине:

\min( {x}^{2} + 8x + 12) = \min(f) = - \frac{b}{2a} = - \frac{8}{2 \times 1} = - 4

ответ: -4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Юлька1150989776543 Юлька1150989776543  18.06.2019 11:00
Перевести в радианную меру 320град 800град...
Вettу Вettу  18.06.2019 11:00
Существуют ли три последовательных четных числа, сумма которых равна 74?...
ivangladkikh ivangladkikh  18.06.2019 11:00
Известно что парабола у=ах2-4х+2 проходит через точку d(3; -1). найдите коэффицент а....
Kirill4421 Kirill4421  18.06.2019 11:00
С1.докажите,что функция f(x)=x^3-cosx+7,является первообразной для функции f(x)=3x^2+sinx. 2.для функции f(x)=2(x+1). а) найдите общий вид первообразных б) напишите первообразную,график...
diman122001 diman122001  18.06.2019 11:00
Представить в виде произведения многочлены: а) mn-mk+xk-xn b) x(2 степень) + 7x-ax-7a в) 3m-mk+3k-k(2 степень) г)xk-xy-x(2 степень)+yk...
lanedaGo lanedaGo  18.06.2019 11:00
106^2-121 122^2-64 черта это дробь а ^2 это степень...
sabrina23052006 sabrina23052006  18.06.2019 11:00
Туманность андромеды удалена от земли на расстояние s~2.3*10(6)световых лет. выразить расстояние s в километрах. нужно...
Юлия45684 Юлия45684  18.06.2019 11:00
15 . исследуйте функцию на четность у=х5-2х3+х...
Jikogogo Jikogogo  18.06.2019 11:00
Вынести множитель за скобку: а) 14ab+49a= б) 84ху²-21х²у= в) -40ах²-8а²= г) b¹⁰-b¹³= д) 36b²-15b= е) 90х⁴у-45ху⁴ ж) -11а²b²+33ab= з) 7а⁴b³-14а³b⁴+21а²b⁵= и) 2а²b²c²-4а²bc²+2a³c...
тигр186 тигр186  18.06.2019 10:50
Решить : 1)найдите область определения функции: а)y=x в квадрате - 3x+4 б)в виде дроби y=6 деленное на x-2 в)в виде дроби y=1деленное на квадратный корень из 6-3х г) y= квадратный...

Популярные вопросы