1. Алгебра
  2. При каком значении a система

При каком значении a система
(a-1)x-y=2
8x+(a-7)y=a-1
имеет бесконечное множество решений?

agent687p0bqk2 agent687p0bqk2    1   16.08.2019 14:33    0

Ответы
ФионаА ФионаА  04.10.2020 23:01

Пусть общий вид линейной системы уравнений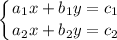 \displaystyle \left \{ {{a_1x+b_1y=c_1} \atop {a_2x+b_2y=c_2}} \right., тогда эта система имеет бесконечно множество решений, если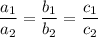 \dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}=\dfrac{c_1}{c_2}

В нашем случае система имеет бесконечно множество решений, когда

\dfrac{a-1}{8}=\dfrac{-1}{a-7}=\dfrac{2}{a-1}

\dfrac{a-1}{8}=-\dfrac{1}{a-7}~~~\Rightarrow~~~ (a-1)(a-7)=-8~~\Rightarrow~~ a^2-8a+7=-8\\ \\ a^2-8a+15=0

По теореме Виета

a=3\\ a=5

\dfrac{a-1}{8}=\dfrac{2}{a-1}~~~\Rightarrow~~~ (a-1)^2=16~~\Rightarrow~~ a-1=\pm4\\ \\ a=5\\ a=-3

-\dfrac{1}{a-7}=\dfrac{2}{a-1}~~~\Rightarrow~~~-a+1=2a-14~~~\Rightarrow~~~3a=15~~\Rightarrow~~ a=5

Из всех что подходит только a = 5.

ответ: при a = 5 система имеет бесконечно множество решений.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
dashkurko1das dashkurko1das  03.02.2021 16:36
Разложите на множители1)a^4-a^62)10n^2+20mn+10m^23)4x^2+24x+36​...
Аминочка8 Аминочка8  03.02.2021 16:36
Докажите, что если a² + b² + c² = ab + bc + ca, то a = b = c....
prodaction2016 prodaction2016  03.02.2021 16:36
Экскурсанты за день км. С утра они шли 5 час(-а), а после обеда — ещё 3 час(-а). Сколько километров экскурсанты утром, если после обеда их скорость снизилась на 1 км/ч. С какой...
Danilove5 Danilove5  18.08.2019 14:40
Найдите значение частного чисел √1.8÷√12.8 равно: 1)8÷9 2)3÷8 3)9÷8 4)8÷3 !...
londi17 londi17  18.08.2019 14:40
Внесите под знак корня: 3√11, -2√6, 5a√a,...
matgim17 matgim17  18.08.2019 14:40
Решить пример : 18^3 / 12^4 это дробь...
agnesa9890 agnesa9890  18.08.2019 14:40
Укажите выражение,равное степени 2^k-3 1)2^k-2^3 2)2^k/2^3 3)2^k/2^-3 4)(2^k)^-3...
Dasha555559 Dasha555559  18.08.2019 14:40
Решить по за седьмой класс 14с• -5сd •3d...
Настюша1118 Настюша1118  18.08.2019 14:40
(4x^2y^5)^2/-(3x^2y^2)^3 /-это начала знаменателя...
svetacok svetacok  18.08.2019 14:40
Выражение (1 - 2с)2 - 4с(с + 1) и найдите его значение при с = -1/4....

Популярные вопросы