При каких значениях x числа образуют арифметическую прогрессию

Согласно свойству арифметической прогрессии: d = a3 - a2 и одновременно d = a2 - a1. Поэтому a3 - a2 = a2 - a1. Итак, a3 = 2a2 - a1.

√(12х+13) = 2√(5х+4) - √х

ОДЗ:

1. 12х+13≥0; х≥-1 1/12

2. 5х+4≥0; х≥-4/5

3. х≥0

ОДЗ: х≥0

(√(12х+13))^2 = (2√(5х+4) - √х)^2

12х+13 = 4(5х+4)-4√(5х+4)√х+х

12х+13 = 20х+16-4√(5х^2+4х)+х

9х+3 = 4√(5х^2+4х)

(9х+3)^2 = (4√(5х^2+4х))^2

81х^2+54х+9 = 16(5х^2+4х)

81х^2+54х+9 = 80х^2+64х

х^2-10х+9 =0

(х-1)(х-9) = 0

х = 1

х = 9

ответ: при х = 1 или х = 9.

ОДЗ:  

             - общее ОДЗ.

1)  Проверим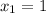  

;          

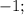
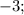
Числа   1;  3;  5;   или  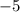      образуют арифметическую прогрессию.

2)  Проверим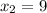  

;          

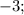
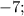
Числа   3;  7;  11;   или        образуют арифметическую прогрессию.

ответ:  {1;  9}