При каких значениях параметра a уравнение имеет ровно два корня?

(-1; 1)

Объяснение:

Заметим, что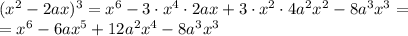

Тогда уравнение имеет вид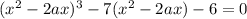

Пусть .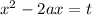

Заметим, что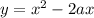 — парабола, ветви которой направлены вверх, с вершиной в точке (a; -a²). Функции y = -2, y = -1, y = 3 — прямые, параллельные оси Ox. Парабола должна пересекать только одну из этих прямых (см. рис.), значит, её вершина по y должна быть между прямыми y = -1 и y = 3: