При каких значениях параметра a неравенство x+2a/x+a+2< 0 выполняется для всех x принадлежит {-1; 0}​

a∈(-1; 0)

Объяснение:

Рассмотрим неравенство .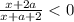

Рассмотрим 3 случая:

1) -2a < -a-2, то есть a>2

Решением будет x∈(-2a; -a-2).

Чтобы для всех x∈[-1;0] неравенство выполнялось, необходимо обеспечить полное вхождение этого отрезка в интервал (-2a; -a-2), то есть:

а) -2a < -1 => a > 0.5

б) 0 < -a-2 => a < -2

Решений для a нет.

2) -2a > -a-2, то есть a < 2

Решением будет x∈(-a-2; -2a).

Чтобы для всех x∈[-1;0] неравенство выполнялось, необходимо обеспечить полное вхождение этого отрезка в интервал (-a-2; -2a), то есть:

а) -a-2 < -1 => a > -1

б) 0 < -2a => a < 0

Получается, что a ∈ (-1; 0)

3)  -2a = -a-2, то есть a = 2. Тогда числитель и знаменатель дроби одинаковы, можно разделить их друг на друга и получить 1. Тогда получим неверное неравенство 1 < 0, то есть неравенство не будет иметь вовсе решений.

Таким образом, получается единственный интервал a∈(-1; 0)