При каких значениях параметра a функция y=(a+2)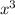 -3a
-3a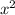 +9ax-2 убывает на R
+9ax-2 убывает на R
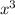
Другие вопросы по теме Алгебра
Популярные вопросы
- Упростите выражение 2/3(4а+15)-2/5(2у-7) и найдите его значение...
3 - Какие острова лишние и почему? (курильские, азорские, канарские)...
2 - Капля масла находится в однородном электрическом поле, на которую...
3 - 4-5. Сөздерді дұрыс орналастырып, қосымшаларды түрлендіріп,...
1 - А) Один из корней квадратного уравнения x^2-mx+27=0 в ти раза...
3 - В первый час автомобиль намеченого пути. Каков намеченый путь,если...
1 - В треугольнике АВС точка М – середина стороны АС, ВМА = 90º...
3 - По рисунку определите, направление силы взаимодействия (притяжение...
3 - Какой фактор увеличивает растворимость твёрдых веществ? Температура...
1 - Какая масса сульфида образуется при взаимодействии 30г железа...
3
a∈(-∞ ; -2)
Объяснение:
Чтобы функция монотонно убывала на R , необходимо и достаточно , чтобы производная этой функции не была положительна для всех x∈R. ( скорость роста функции всегда не положительна , то есть идет постоянное убывание . y'<=0 )
y=(a+2)*x^3 -3*a*x^2 +9*a*x -2
Параметр a является константой и дифференцируется подобно константе.
y'=3*(a+2)*x^2 -6*a*x +9*a - квадратный трехчлен (парабола)
Парабола не положительна при всех значениях x тогда и только тогда ,когда ее дискриминант не положителен (D<=0) и ветви параболы идут вниз ( 3*(a+2)<0 → a<-2)
D/4 = 9*a^2 -27*(a+2)*a <=0
a^2 -3*a*(a+2)<=0
a* (a -3*(a+2) ) <=0
a* (-2a-2) <=0
a*(a+1)>=0
a<-2
a∈(-∞ ; -2)
Рассмотрим отдельно случай понижения степени функции : a=-2
y'= 12*x-18 - данная функция может быть положительна.
ответ : a∈(-∞ ; -2)