При каких значениях m уравнение mx-2=m^2-5m+4
a) имеет единственный корень
б) не имеет корней
в) имеет бесконечно много корней

Question

Алгебра: При каких значениях m уравнение mx-2=m^2-5m+4 a) имеет единственный корень б) не имеет корней в) имеет бесконечно много корней

shchetko2006p013vy · Answer

Объяснение: Перепишем уравнение в следующем виде:

mx = m² - 5m + 4 + 2, mx = m² - 5m + 6

Если m = 0, то имеет: 0 · x = 0 - 0 + 6, 0 = 6 - неверное равенство. Следовательно, при m = 0 уравнение не имеет решений.

Если m ≠ 0, то уравнение имеет единственное решение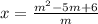 $x = \frac{m^2-5m+6}{m}$

Значений m, при которых уравнение имеет бесконечно много корней, не существует.