При каких значениях "a" неравенство 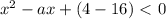не имеет решение

a=8

Объяснение:

x²-ax+(4a-16)<0

Допустим:

x²-ax+(4a-16)=0

D=a²-4·(4a-16)=a²-16a+64=(a-8)²

x₁=(a-a+8)/2=4

x₂=(a+a-8)/2=a-4

a-4<x<4; a<8

4<x<a-4; a>8

Отсюда следует, что неравенство не имеет решений при a=8.

рассмотрим квадратный трехчлен х²-ах+(4а-16),  его первый коэффициент равен 1, а дискриминант D=а²-4*1*(4а-16)=а²-16а+64=(а-8)²

т.к. графиком квадратичной функции у= х²-ах+(4а-16) является парабола, ветви которой направлены вверх, то неравенство

х²-ах+(4а-16) <0 не будет иметь решений, когда парабола будет находиться выше оси ох, или будет касаться оси ох,  а это достигается, когда дискриминант меньше нуля  или равен нулю, но (а-8)²≥0 при любом значении а, значит, при а=8   неравенство не   имеет решения.

ответ при а=8.