При каких значениях а многочлен P(x) имеет корень равный
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) какие функции выполняют покровные ткани?...
1 - (1/(x-1)^2)+(2/(x-=0 нужно полное решение...
2 - По плану туристы должны были пройти 20 км за 5 часов но они это расстояние на 1...
1 - Хорда cd окружности пересекает её диаметр ab в точке m. известно, что cm=5 см, md=3...
3 - Найдите значение k,при котором график функции y=-1/6x+k проходит через точку м (4;...
1 - Разгадай правило по какому составлены схемы выпиши пропущенные найди числа...
2 - Напишите программу которая будет переводить из 10 системы с счисления в любую другую...
2 - Вкакой части европы расположены самые высокоразвитые в отношении страны? что это...
1 - Марина вышила картину на полотне квадратной формы со строной 25 см.она попросила...
3 - Есть число 3656158440062976. распишите его. (столько-то едениц ,десятков ,сотен...
2
Если х=2 - корень многочлена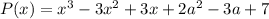 , то
, то
P(x)=x³-3x²+3x+2a²-3a-7
P(2)=2³-3·2²+3·2+2a²-3a-7 = 8-12+6+2a²-3a-7 = 2a²-3a-5
P(2) = 2a²-3a-5
P(2) = 0
2a²-3a-5 = 0
D = 9 - 4·2·(-5) = 9+40 = 49 = 7²
a₁ =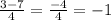
a₁ = - 1
a₂ =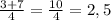
a₂ = 2,5
ответ: - 1; 2,5