Постройте график функции у=(х-1)^2-1 найдите "нули функции".
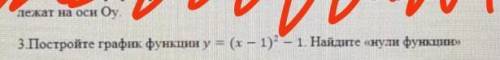
Другие вопросы по теме Алгебра
Популярные вопросы
- Соединить прилагательное с подходящими по смыслу существительным каменное...
2 - Четыре ученика при нахождении значения числового выражения (4800: 16-12)х5...
2 - Два отряда туристов вышли од-новременно на встречу друг другу из двух школ....
2 - Сила аэростата заполненного гелием равна 1 вычислите объем гелия если масса...
1 - Вexcel таблицу значений функции двух переменных f(x,y), в прямоугольной...
1 - Скласти речення з одним словом щоб воно виступало іменником а в другому...
1 - Самое глубокое место аральского моря 68м выразить глубину в дециметрах...
2 - Расположи события в хронологической последовательности. 1) избрание на царство...
1 - Какие почвы в крыму являются вредными для растений и следовательно непригодный...
3 - Два точечных электрических заряда на расстоянии r взаимодействуют с силой...
3
1. Начнем с построения осей координат. Они должны быть перпендикулярны друг другу и проходить через точку (0, 0).
2. Затем отметим на графике точку (1, -1), так как это единственная известная нам точка функции.
3. После этого мы можем построить параболу, потому что функция у=(х-1)^2-1 является квадратичной функцией. Квадратичная функция имеет форму параболы и описывается уравнением у=a(х-h)^2+k, где а - коэффициент, определяющий ширину открытия параболы, (h, k) - координаты вершины параболы. В данном случае а = 1, h = 1, k = -1. Вершина параболы будет находиться в точке (1, -1).
4. При помощи вершины параболы, мы можем построить параболу. В данном случае парабола будет открываться вверх, потому что коэффициент а равен 1. Если бы коэффициент а был отрицательным числом, парабола бы открывалась вниз. Начиная с точки (1, -1), мы можем провести путь параболы, подбирая другие точки.
5. Нули функции являются точками, где график пересекает ось x. Чтобы найти эти точки, мы должны решить уравнение у=(х-1)^2-1=0. Раскрывая скобки и приводя подобные слагаемые, мы получаем: у=(х^2-2х+1)-1=0. Далее, объединяя похожие слагаемые, мы получаем: у=х^2-2х=0. Затем мы можем разложить это уравнение на множители и получить уравнение (х-2)(х-0)=0. Таким образом, у нас есть два возможных значения для х: х=2 и х=0.
6. Чтобы подтвердить наш ответ, мы можем подставить х=2 и х=0 обратно в исходную функцию и убедиться, что они равны 0. Если оба значения дают 0, то это является правильным ответом.
7. Наконец, мы можем отметить на графике две точки, где функция пересекает ось x: (2, 0) и (0, 0).
Таким образом, мы построили график функции у=(х-1)^2-1 и нашли "нули функции" в точках (2, 0) и (0, 0).