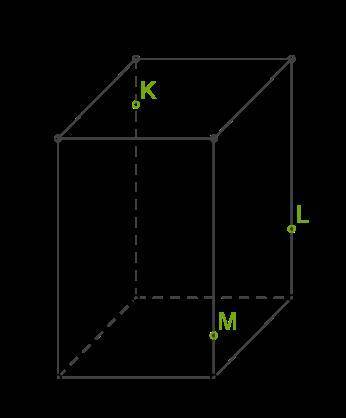
Построй прямую пересечения верхнего основания параллелепипеда с плоскостью, которая проходит через точки M, K и L.

Для того чтобы построить прямую пересечения верхнего основания параллелепипеда с плоскостью, проходящей через точки M, K и L, нам понадобятся некоторые геометрические знания и инструменты.

1. Взглянем на данную нам фигуру и обратим внимание на то, что прямая пересечения верхнего основания параллелепипеда с плоскостью будет параллельна линии пересечения передней и задней граней параллелепипеда.

2. Нам необходимо определить две точки на этой прямой. В качестве первой точки мы можем выбрать саму точку M, так как она уже задана.

3. Для определения второй точки на прямой будем использовать линейку. Установим линейку так, чтобы она проходила через точки K и L. Подвигая линейку вдоль этой линии, найдем точку пересечения линейки и верхнего основания параллелепипеда. Обозначим эту точку как N.

4. Теперь у нас есть две точки на прямой - M и N.

5. Для построения прямой, проходящей через эти две точки воспользуемся циркулем. Возьмем циркуль и установим его одно конечное ухо на точку M, а другое - на точку N. Затем, сохраняя расстояние между этими точками, проведем дугу с циркулем.

6. Теперь, продолжая дугу, устанавливаем второе конечное ухо циркуля на точку N и проводим аналогичную дугу.

7. Точка пересечения этих двух дуг будет лежать на прямой, которую мы и искали. Обозначим эту точку как P.

8. Продлим прямую, проходящую через точки M и P, чтобы она пересекала верхнее основание параллелепипеда. Обозначим точку пересечения как Q.

Теперь мы построили прямую пересечения верхнего основания параллелепипеда с плоскостью, которая проходит через точки M, K и L.