1. Алгебра
  2. Последовательность задана

Последовательность задана формулой n-го члена аn=1/4(n-7)2 Определить ,под каким номером в эту послед. Входит число 16

anastasia106444 anastasia106444    2   23.07.2021 18:27    5

Ответы
Katyastudio Katyastudio  23.07.2021 18:30

15

Объяснение:

16 = \frac{1}{4}(n-7)^2\\16*4=(n-7)^2\\64=n^2-14n+49\\n^2-14n-15=0

Можно решить через дискриминант:

D=(-14)^2 - 4*1*(-15)=196+60=256=16^2\\n_1=\frac{-(-14)+\sqrt{16^2}}{2*1}=\frac{14+16}{2}=15\\n_2=\frac{-(-14)-\sqrt{16^2}}{2*1}=\frac{14-16}{2}=-1

Можно решить через теорему Виета (так как коэффициент при n^2 равен 1):

\left \{ {{n_1+n_2=-(-14),} \atop {n_1*n_2=-15;}} \right. \\\left \{ {{n_1+n_2=14,} \atop {n_1*n_2=15.}} \right.

Путём подбора находим корни n_1=15,~~n_2=-1

Поскольку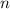 n должно быть натуральным числом (нет -1-го члена у последовательности), подходит только 15. Проверим:

\frac{1}{4}(15-7)^2=\frac{1}{4}*8^2=\frac{1}{4}*64=16

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Alina9392010 Alina9392010  17.03.2019 07:50
Можно ли назвать возрастающей последовательность : а)1,-2,3,-)1,1,2,2,3,...
alina1922 alina1922  17.03.2019 07:50
Увеличив радиус окружности, длину окружности увеличили на 20%. на сколько процентов увеличили её радиус?...
frossbaf frossbaf  17.03.2019 07:50
Найти корни уравнения sin(3x-pi\6)=1\2...
Информатик111111 Информатик111111  17.03.2019 07:50
Решите систему уравнений: {xy=4, {2x-y=-2; №2 решите систему уравнений: a){x^2+y^2=25; б){x^2y^2-xy=12; {x+y=7. {x+y=2....
logoschaolj logoschaolj  17.03.2019 07:50
Втупоугольном треугольнике abc ab=bc,угол а равен 30 градусов,сd - высота, проведённая из вершины с.найдите градусную меру угла bcd....
ДинаLovE123 ДинаLovE123  17.03.2019 07:50
Найдите 26sin(п/2+а), если sina=-5/13 и а принадлежит ( п/2; п)...
Djajdjo Djajdjo  17.03.2019 07:40
Решить уравнение (3x-1)(12x+1)-10=(6x+2)^2...
MafiiMan7204720 MafiiMan7204720  17.03.2019 07:40
Представьте в виде суммы выражения: 1)15а-9 2)а-b-c 3)x-3y 4)1/x-1/y-1/z...
ivantretyak02 ivantretyak02  17.03.2019 07:40
Прямая у=кх+б проходит через точки а(3; 3) и в (-1; -5). найдите величины к и б. нужно решение и ответ....
ЛилияСадыкова555 ЛилияСадыкова555  17.03.2019 07:40
и как можно скорее! 1)известно, что sin t=-0,28 π...

Популярные вопросы