понять разъяснение в учебнике Задание: Довести, что при любом натуральном n значение выражения есть квадратом натурального числа
Вот решение, данное в учебнике :
на этих 3 этапах всё ясно
НО
здесь уже ничего не понятно. пример, показанный ранее и сейчас - это равные части уравнения, но когда я расклад на множители, я не увидит этого равенства. так же откуда взялось (n2 + 3n)2, а вместе с ним и 2(n2 + 3n)
потом эту кучу как-то привели к виду (n2+3n+1)2. n2 + 3n- просто сократили, но почему в примере стоит ещё и квадрат? откуда здесь единица и куда делать двойка из уравнения
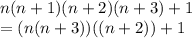
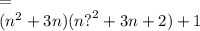
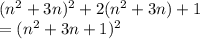
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
- Преобразуйте предложения в вопросительную, отрицательную и утвердительную...
1 - Какая площадь шарика для теннисного стола...
2 - Вчём значимость путешествия васко да гамы в индию...
2 - Сколько сигма и пи связей в йодид фосфора 5, оксибромид фосфора и оксид...
2 - Какой объем оксида углерода (iv)(при н.у.)образуется при сгорании 3 моль...
3 - Сответом! птица дрофа занесена в красную книгу. какие причины исчезновения?...
3 - Осуществите превращения k kob kcl kno3 o2 co 2 ...
2 - Содержит наследственную информацию, обеспечивает сходство материнской...
3 - Сколько минут содержится в 1/5 часе, в 5/4 часе, в 2/3 часе, в 11/10 часе?...
3 - Сделайте противоположность ...
3