Помагите, очень надо 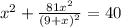
х^2+81х^2\(9+х) ^2=40
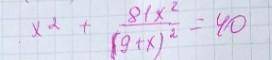
Другие вопросы по теме Алгебра
Популярные вопросы
- 214. а) Длины сторон двух участков земли, имеющих форму ква- драта, равны...
1 - Пропись 1 класс 4 часть горецкий федосова ФГОС ответ стр32...
1 - Давление- величина, равная относнию нисилы, действующей перпендикулярноповерхности,...
1 - На місці крапок поставте е(є) чи о(ьо), йо Гуртк..ва робота, м’яз..ва напруга,...
1 - Fill in the correct adverb, then say how we form adverbs.sudden loud final...
2 - С2 - d2 при с=при c = V3 + 4 и d=V 3 - 4...
1 - Награда: Вопрос мне очень нужно за правильный ответ. Тип: Математика. Фотоматериалы:...
1 - География заполнить таблицу...
1 - с этим и я всегда даю только 10б потому что сейчас у меня 20...
1 - 847.объём прямоугольного параллелепипеда 1248 см3. Ето а ширина 8 см. Найдите...
1
Объяснение:
воспользуемся равенством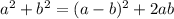
тогда
действительных корней не имеет