Покажите, являются ли события A и B зависимыми или независимыми, если P(A) = 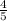 , P(B)=
, P(B)=  , P(A⋂B)=
, P(A⋂B)= 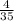
Другие вопросы по теме Алгебра
Популярные вопросы
- К+7 если к=4 к=9 к=6 найти значение виразу...
1 - This is what the children planned to do to help people in their...
2 - Она бросила [й,иво] мне на диван и сказала хороший мишка, отличный.ишь,как...
3 - С, . я не блещу, а переводчик пишет не так, как надо (коряво), а...
1 - Почему византия, страны и западноевропейские крестоносцы потерпели...
1 - Это вещество входит в состав любого живого организма...
3 - Діалог між семикласницею та її п ятирічною сестрою якій наснився...
3 - Как мангуст перехитрил крокодила и леопарда это самая древняя сказка?...
3 - Представители какого отдела грибов никогда не образуют плодовых...
3 - Найти 9 слов в цепочке из букв по языку...
3
Если события A и B являются независимыми, то вероятность их пересечения равна произведению вероятностей каждого события в отдельности: P(A⋂B) = P(A) * P(B).
В нашем случае, P(A) = 4/5, P(B) = 4/7 и P(A⋂B) = 4/35.
Проверим решение:
P(A) * P(B) = (4/5) * (4/7) = 16/35
Таким образом, P(A⋂B) не равно P(A) * P(B), следовательно, события A и B являются зависимыми.