Показательные неравенства решите задачу, и с объяснениями каждого шага(если не сложно)
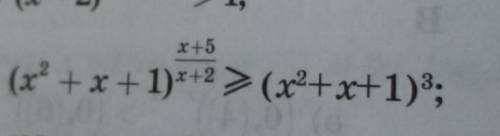
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить падеж прилогательного в предложении. наступила ранняя...
1 - Выбери праверочные слова покажи правильность своего выбора глаз- глаза ,глазной...
1 - Составте небольшой рассказ на тему: все получилось или все получится...
1 - 6)изучите таблицу и определите какой пациент (а или б) страдает сахарным диабетом....
2 - Как обращение обозначается в предложении...
2 - Сколькими в бригаде из шести операторов можно распределить три путевки в профилакторий,...
1 - Пять слов разделительным твердым знакам...
3 - Надо написать сообщение о вирусах в 5 предложениях....
3 - 10.верны ли следующие суждения о заработной плате? а. заработная плата – цена...
2 - Какое спряжение у глаголов: тихий,город,ночной,держать,может,листва,тревожить,разносить,фея,болит,шагать,старый,сторож,толстой,палкой,квартал....
1
рассмотрим два случая:
1) когда основания < 1 (знак меняется)
2) > 1, знак остаётся прежним
1.
пересекаем оба решения:
2.
пересекаем:
объединяем два решения: