Показательные неравенства подробно
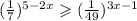
Другие вопросы по теме Алгебра
Популярные вопросы
- Предварительный просмотр: Контрольная работа (тестирование) по теме «Имя...
2 - Як географічні чинники вплинули на результати Кримської війни...
1 - Знайдіть площу трикутника зі сторонами: б) 15, 26 і 37(геометрія 9 класс)...
2 - Тапсырма № 6 Шығармашылық тапсырма1. Құмырсқа сөзіндегі әріптерді пайдаланып...
2 - задание по математике сделать !...
3 - Высота классной комнаты 5 м Сколько времени будет падать шарик от потолка...
3 - 2. Які часи відображені в поемі Євшан-зілля ?3. Як до князя Володимира потрапив...
2 - Какие из точек А(6;-2), В(-4;3), С(0;0), К(8;4), М(-7; 3,5) принадлежат...
3 - Чому слід вивчати біологію окремих паразитів...
3 - ЗАРАНИЕ Дайте характеристику вірша «Лицарі і Дами» Алан Мілн або іншого...
2
Объяснение:
ответ: x∈(7/8;+∞).