Подставляю, выражаю, дальше чушь получается.. найдите четыре целых числа, из которых первые три составляют прогрессию, а последние три составляют арифметическую прогрессию, если известно, что сумма двух средних чисел равна 12, а сумма двух крайних чисел равна 14.

Решение: Пусть a,b,c,d – данные последовательно записанные числа. Тогда по условию

a+d=22    (1)

b+c=20    (2)

Из свойств арифметической и геометрической прогрессии имеем:

a+c=2*b (3)

c^2=b*d (4)

Из (2) получим b=20-c (5).

Сложив (1) и (2), получим a+b+c+d=22+20=42, использовав (3) и (5), получим

3*b+d=42, d=42-3*b=42-3*(20-c)=42-60+3*c=3*c-18, то есть

d=3*c-18 (6).

Использовав (4), (5), (6), получим

c^2=(20-c)*(3c-18). Решаем:

c^2=60*c-360-3*c^2+18*c=-3c^2+78c-360.

4*c^2-78*c+360=0

2*c^2-39*c+180=0.

d=39^2-4*2*180=81

c1=(39-9)\(2*2)=30\4=15\2=7.5

c2=(39+9)\(2*2)=12

Из (1), (6) получим

а=22-d=22-(3*c-18)=40-3*c (7).

Используя (5), (6), (7), получим

a1=40-3*7.5=17.5

a2=40-3*12=4

b1=20-7.5=12.5

b2=20-12=8

d1=3*7.5-18=4.5

d2=3*12-18=18

Таким образом получили две последовательности 17.5;12.5;7.5;4.5 и

4;8;12;18

ответ: 17.5;12.5;7.5;4.5 или 4;8;12;18

прощения, но решение получилось слишком сложным :(

q - знаменатель геом. прогр.

d - сумма арифм. прогрессии

a - первый член ар. прогр.

b - первый член геом. прогр.

1) a+d+a+2d=2a+3d=12;  также b+bq=b(1+q)=12; также bq+a+d=12 

2) a+2d=bq

3) a+d=b

4) a+bq^2=14

из b(1+q)=12:

из a+2d=bq и a+d=b выражаем b+d=bq -> d=bq-b=b(q-1)

т.е.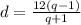  

из a+bq^2=14 выразим a=14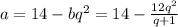 

Подставим в 2a+3d=12 получим квадратное уравнение вида:

После всех приведений и сокращений и с учетом, что занменатель д.б. не равен 0, получим:

Решая єто уравнения получим, что q=5/3 - не подходит, т.к. в условии числа д.б. целыми и q=1/2.

Отсюда b=8, a=12, d=-4

Получаем последовательность:

12   8   4   2