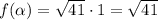подскажите, как найти найбольшее значение примера , с объяснением. заранее )
Другие вопросы по теме Алгебра
Популярные вопросы
- унаслідок пропускання вуглекислого газу крізь розчин барій гідроксиду масою...
3 - там внизу нужно дополнить предложения...
1 - Перепишите, употребите сказуемые с отрицанием не и прямые до- полнения в...
2 - за лёгкую упражнение плз пацаны....
2 - Табиғатқа байланысты мамандық...
1 - А.с- кем? не? төстік,ертегі, ешбірі, заман. У.с-тостіктіңТ.с-Б.с-Ж.с-Ш.с-К.с-...
3 - Мне нужна харектиристика речки Мурей На Український мов...
2 - 1. Какое количество кислорода и азота в воздухе? может быть определено2....
1 - Скільки молекул повітря знаходится у приміщенні розміром 5x4x3 м за температури...
1 - Алгебра 8 КЛАСС решить уравнение...
2
Объяснение:
Воспользуемся методом вс аргумента:
Введем функцию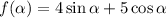
Пусть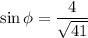 и
и 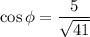
Так как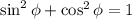
По свойствам функции синус она достигает максимального значения 1, тогда максимум функции