Подскажите , как это решать? только подробнее. не могу разобраться с ответом
(1 - x)} \geqslant 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько будет a+b•2 если a=2100 а b=200...
2 - 1. определите молекулярные формулы галогенопроизводных углеводородов этана c2h6...
2 - 1)к данным словам,где возможно,подберите антонимы,запишите их парами! 2)какие значение...
3 - Каковы особенности климата в индии? как они влияют на занятие сельскимхозяйством...
2 - Стоимость проезда в пригородном электропоезда составляет 198 рублей. школьникам...
3 - Карлсон съел треть плюшек, которые испекла фрекен бок, и после этого осталось 12...
2 - Масса брома, необходимого для получения 47 г дибромэтана из этана,...
2 - Придумайте ситуацию, когда на тело перестанет действовать архимедова сила? please))...
1 - Рассмотрим натуральное а с ненулевой последней цифрой. через в обозначим а, записанное...
2 - Объясните смысл понятий общественная территория...
1
ОДЗ: знаменатель дроби не должен обращаться к нулю
Решив уравнение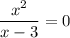 получим
получим 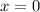
ответ: x ∈ (-∞;1) ∪ (1;3)