Под строительную площадку отвели участок прямоугольной формы, длина которого на 30 метров больше его

Question

Алгебра: Под строительную площадку отвели участок прямоугольной формы, длина которого на 30 метров больше его ширины. при утверждении плана застройки выяснилось, что граница участка проходит по территории водоохранной зоны, поэтому его ширину уменьшили на 20 метров. найдите длину участка, если после утверждения плана застройки площадъ участка составила 2400м в квадрате. решить !

Хаченок1337 · Answer

Пусть ширина площадки - А... Тогда из условия видно, что площадку сначало увеличили на 30, а потом уменьшели на 20 <=> B (Ширина) = А+10

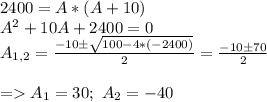
По условию S = 2400, а также S = А*B =>
$2400 = A*(A+10)\\ A^{2} +10A +2400 = 0\\ A_{1,2} = \frac{-10б \sqrt{100 - 4*(-2400)}}{2} = \frac{-10б 70}{2}\\ \\ = A_{1} = 30; \ A_{2} = -40\\$
Но растояние не может быть меньше нуля... => А = 30

=> B = 40

ОТВЕТ: 40

Популярные вопросы