Почему пример:
x*(x-1)=0
можно решить вот так
x=0
x-1=0
x=1
ответ: x1=0,x2=1.
а например пример
x*(x-1)=2 таким решить нельзя.

​

Произведение равняется нулю, когда хотя бы один один из множителей равняется нулю.

В данном случае множителей два:

первый: , а второй: .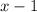

Поэтому мы их и приравниваем по очереди к нулю, то есть:

1)

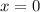
2)

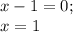
Если икс будет равен нулю или единице, то мы точним получим ноль в решении.

Замечу, что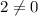 (это - разные числа), следовательно, правило, описанное выше, не подходит. Оно подходит только (!) если после равно стоит ноль и выполняется действие умножения (а не вычетаниея, как, например, записано чуть ниже, сложения или деления).

Это уравнение решается таким

1) переносим двойку в левую часть с противоположным знаком (был "+", перенесли, стал "-")

(тут у нас уже НЕ умножение, а вычетание, т.к. мы отнимаем двойку, значит, тот метод НЕ подходит)

Раскрываем скобки:

По теореме Виета для уравнения:

То есть для нашего уранвения:

Подбираем их, вспоминая таблицу умножения. Такими числами являются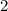 и .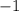

Действительно:

Cледовательно