Почему при решении уравнения 3sqrt(x + 3) - sqrt(x - 2) = 7 появляются посторонние корни (x = 33/16), которые даже в ОДЗ входят? И как эти посторонние корни отсеять без их подстановки в исходное уравнение?
Другие вопросы по теме Алгебра
Популярные вопросы
- А) 2/3 + 1/4 б) 4/5 - 3/4 в)1/2 -1/3 г)5/6 + 3/8...
1 - Образовать множественное число knife,day,toy,sleep...
1 - Найдите неизвестное число: 12,8-x=3,75....
1 - Какая это скороговорка грачиха говорит грачу: слетай с грачатами к врачу. прививки...
2 - 6т 369 кг: 3=__т__кг 42 руб 72 к: 6= 2 км 112 м: 2=__км__м 24 м 12 см: 4=__м__см...
1 - Население индонезии (общая численность населения, тип воспроизводства, национальный...
2 - Сколько звезд в созвездии дракон,лебедь,кассиопея?...
3 - Чему равна разность самого наибольшего двузначного числа и наименьшего двузначного...
3 - На поляне играет оркестр. в нем несколько белочек играет на трубах, а зайчиков-барабанщиков...
2 - Каково ваше мнение. стоит ли развивать сельское хозяйство в россии или лучше перейти...
3
(см. объяснение)
Объяснение:
Решим уравнение "школьным" :
Рассмотрим первую строку системы:
Запись справа от равно неотрицательна (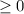 ).
).
Тогда, если слева окажется отрицательное число, корней не будет.
Поэтому равносильным переходом станет:
Рассмотрим первую строку системы:
Но у нас есть условие, что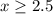 , откуда
, откуда 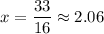 не подходит.
не подходит.
Тогда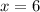 - это корень уравнения.
- это корень уравнения.
Уравнение решено!