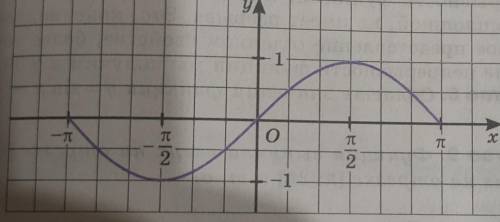
Почему на фото между π/6 и 5π/6 период равен 2π/3? Ведь период должен быть 2π

Ответы

Holmes9 25.11.2021 06:40

Между π/6 и 5π/6 расстояние равно 5π/6-π/6=4π/6=2π/3 .

Период функции y=sinx равен Т=2π , поэтому

$sin\dfrac{\pi}{6}=sin\Big(\dfrac{\pi}{6}+2\pi \Big)=sin\dfrac{13\pi }{6}=\dfrac{1}{2}sin\dfrac{5\pi}{6}=sin\Big(\dfrac{5\pi}{6}+2\pi \Big)=sin\dfrac{17\pi }{6}=\dfrac{1}{2}$

На картинке расстояние 2π равно между точками с абсциссами 5π/6 и -7π/6, поэтому

$sin\dfrac{5\pi}{6}=sin\Big(\dfrac{5\pi}{6}-2\pi \Big)=sin\dfrac{-7\pi }{6}=\dfrac{1}{2}$

Почему на фото между π/6 и 5π/6 период равен 2π/3? Ведь период должен быть 2π

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Nastya0012005 02.03.2019 16:30

Сумма двух смежных углов прямоугольника равна 27 см. найдите стороны прямоугольника зная,что площаь равна 180см2...

aimnura73 02.03.2019 16:30

Преобразуйте в многочлен стандартного вида (2x+1)2-(x-5)(x+5)...

katttty9989 02.03.2019 16:30

Найдите периметр прямоугольного треугольника, если его гипотенуза равна 25, а один из катетов на 17 больше другого....

ГришаМститель 02.03.2019 16:30

Мне, ! можно не все сразу, по отдельности! 1) составьте квадратное уравнение, корни которого на 3 меньшекорней уравнения х^2+8х-1=0. 2) составьте какое-нибудь квадратное уравнение,...

stefaniiadr 02.03.2019 16:30

1) tg27°*tg63°= 2) arcctg(-sqrt3)+arccos(-sqrt3\2)+arcsin1= 3) sin73°-sin36°= 4) xctg^2(-30°)-18sin(-30°)=sin360°...

kuzminasasa64 02.03.2019 16:30

X3+125y3\ 1-27y3 0.001x3-8y3 x3y9+343...

Maksim24k 02.03.2019 16:30

Известно, что х/у=10. найдите значение выражений х+4у/у....

MissKaprizz99 02.03.2019 16:30

1) x3+125y3 2)1-27y3 3)0.001x3-8y3 4)x3y9+343...

lisena4555 02.03.2019 16:30

Поезд путь от одной станции до другой за 3,5 ч со скоростью 70 км/ч. с какой скоростью должен был бы идти поезд, чтобы пройти этот путь за 4,9 ч?...

RomanovDanya201DAnua 02.03.2019 16:30

Впервый день автомобиль проехал 425км что на 83км больше чем во второй день в третий день автомобиль проехал на 58км больше чем в первый день сколько километров проехал автомобиль...

Почему на фото между π/6 и 5π/6 период равен 2π/3? Ведь период должен быть 2π

Популярные вопросы