,
Побудуйте графіки функцій
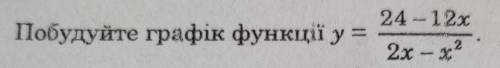
Другие вопросы по теме Алгебра
Популярные вопросы
- Что человек должен делать для сохранения природных богатств 5 примеров. молю...
1 - Запишите каждую из дробей в виде частного 27/31 28/75 65/200...
2 - Іть дібрати 3 запитання до товору федько-халамидник в. винниченко...
1 - Установите соответствие между функциями и их графиками.функцииб) уb) у = - 2x2...
3 - Що я роблю в школі на уроках (розповідь на мові 3- 4 речення для дитини в 2...
3 - Много ! запросы к поисковой системе: 1) бульдог/доберман/уход 2) бульдог/доберман/уход/питомник...
3 - Сочинение на тему человек который держит свое слово. составьте 6-7 предложений!...
2 - Приготовить 50 мл 25% р- раз из 95% р-ра .если что речь идёт о кислоте . там...
1 - Вероника загаывает число от 1 до 5. рита и таня пытаются угадать его,записывая...
1 - Выведите простейшую формулу сернистого железа, зная его процентный состав (по...
1
Объяснение:
Разложим на множители выражение в числителе и знаменателе.
\begin{gathered}y=\frac{24-12x}{2x-x^2}\\y=\frac{-12(x-2)}{-x(x-2)}\\\left \{ {{y=\frac{12}{x} } \atop {x\neq 2}} \right.\end{gathered}
y=
2x−x
2
24−12x
y=
−x(x−2)
−12(x−2)
{
x
=2
y=
x
12
Это гипербола, которая лежит в 1 и 3 четверти и имеет асимптоты, которыми являются оси координат.
Отметим 2 точки, которые принадлежат этой функции на координатной плоскости для более точно построения.
x=12 --> y=1; (12;1)
x=1 --> y=12; (1;12)
И проведём через них нашу гиперболу.
Да
Объяснение:
24-12x =12х
2х_х2=0х
Не знаю не уверена что правильно