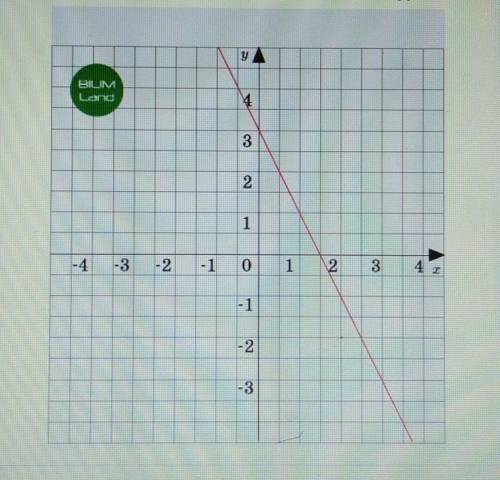
По графику линейной функции, изображенному на рисунке, напиши уравнение прямой. у=-2х-3
у=-3х+2
у=2х+3
у=-2х+3
Другие вопросы по теме Алгебра
Популярные вопросы
- 3. На координатной плоскости постройте график прямой пропорциональности...
2 - все часы на рисунке показывают разное время но только на одних часах время...
1 - Путешествие в будущее не за горами. E. Велтистов «Миллион и один день...
1 - 3 Make sentences using the phrases in the chart. Then explain your ideas...
3 - 800 +90+8=200 +30 +5=500+40 AGF100абозо+3—...
3 - у меня соч надо сделать до...
1 - Б) В треугольнике один из внутренних углов равен 46°, а один из внешних...
1 - Взаимоотношения сарматов с соседями, Римом, скифами (по 3 предложения)....
1 - Выписать элементы фантастики и реальности из рассказа Как растут ёлочные...
3 - A) ә) 9xy 5a²6 c+d c-d a 3х2 c²+cd 2c²-2d²...
3
Сначала определим коэффициент наклона прямой. Коэффициент наклона (обозначенный как "а" в уравнении у = ах + b) показывает, насколько изменяется значение "у" при изменении значения "х".
Нам дан график, где прямая проходит через две точки: (-2, 1) и (2, -5). Чтобы найти коэффициент наклона, мы должны использовать формулу:
а = (y2 - y1) / (x2 - x1),
где (х1, у1) и (х2, у2) - координаты двух точек на прямой.
Для точек (-2, 1) и (2, -5) у нас будет:
а = (-5 - 1) / (2 - (-2)) = (-6) / (4) = -3/2.
Теперь мы знаем, что коэффициент наклона равен -3/2.
Затем определим свободный член (обозначенный как "b" в уравнении у = ах + b). Свободный член показывает значение "у", когда "х" равно нулю. Для этого мы можем использовать любую из точек на прямой. Возьмем точку (-2, 1):
у = ах + b,
1 = (-3/2)(-2) + b,
1 = 3 + b,
b = 1 - 3,
b = -2.
Теперь мы знаем, что свободный член равен -2.
Таким образом, уравнение прямой, изображенной на графике, будет:
у = (-3/2)х - 2.
Ответ: уравнение прямой - у = (-3/2)х - 2.