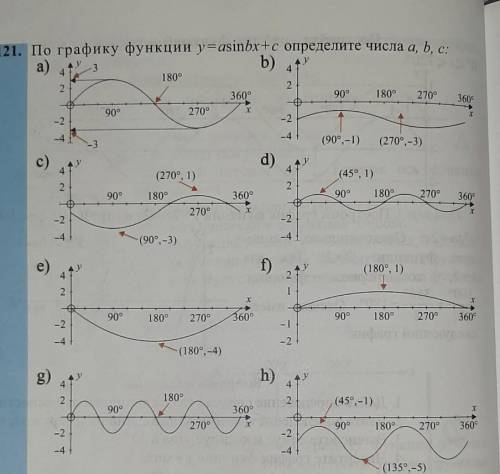
По графику функции y=asinbx+c определите числа a,b,c

Для определения чисел a, b и c в функции y = asin(bx) + c, мы можем использовать информацию, предоставленную в графике.

1. Определение числа a:
a отвечает за амплитуду функции, т.е. высоту пика относительно оси x. В данном графике, максимальное значение функции достигается в точке (0, 2) и (-π, -2), а минимальное - в точке (π, -2).

Так как максимальное и минимальное значения функции составляют 4 величины (2 - (-2) = 4), то a = 2.

2. Определение числа b:
b отвечает за период функции, т.е. расстояние между одним полным колебанием функции. В данном графике, мы видим, что одно полное колебание функции происходит за период от точки (0, 2) до (-π, -2) и обратно до точки (π, -2).

Таким образом, период функции равен 2π, и, учитывая формулу периода, b = (2π) / период = (2π) / 2π = 1.

3. Определение числа c:
c отвечает за вертикальный сдвиг функции вверх или вниз. В данном графике, мы видим, что функция пересекает ось x в точке (π/2, 0).

Таким образом, с = 0.

Итак, мы получили, что числа a = 2, b = 1 и c = 0. Финальная формула функции становится y = 2sin(x) + 0, что сокращается до y = 2sin(x).