Площадь треугольника равна 1 каждая его сторона отмеченными точками делится на равные части. Найдите площади закрашенных фигур
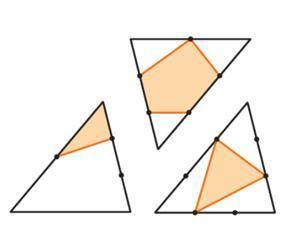
Другие вопросы по теме Алгебра
Популярные вопросы
- Для прорастания большинства семян необходимы вода, свет, почва свет, воздух,...
1 - Из системы уравнений x+2y-3z=52x-y-z=1x+3y+4z=6 найти значение y...
1 - 7Запиши уравнения и реши их.а) Разность 17 214 и неизвестного числа равна...
2 - 24. 6. Грунти, які переважають на території, прилеглій до Чорного й Азовського...
3 - А) Какие основные образы СС. Прокофьев отображал в своих произведениях?...
3 - Які з цих речовин малорозчинні у воді: 1) натрію гідроксид; 2) арґентум...
3 - Каким климатическим поясам соответствует климатограммы? А) 1-Субтропическому...
3 - Прочитайте стихотворения Н.М.Рубцова «Ночь на родине», «Тихая моя родина»,...
2 - Критерії для порівняння Індії і Пресії....
1 - 1.Укажіть речення, у якому відокремлена обставина виражена іменником з...
1
Дано, что площадь треугольника равна 1. Площадь треугольника можно выразить через его стороны и высоту, поэтому нам нужно найти значения этих параметров.
1. Начнем с точки A. Дано, что точка А делит сторону BC на две равные части. Обозначим точку деления как D.
Теперь, обратимся к высоте треугольника. Высота опускается из вершины A и перпендикулярна основанию BC. Пусть точка, где высота пересекает BC, обозначается как H.
2. Так как точка A делит сторону BC на две равные части, то вектор AD должен быть равен вектору DC. Это означает, что отрезок CD имеет такую же длину, как и отрезок AD.
Обозначим каждую равную часть стороны BC как x. Тогда длина отрезка AD равна x, а длина отрезка CD также равна x.
3. Далее, мы можем заметить, что треугольник ABC состоит из двух треугольников: ADD' и BDC. Площадь треугольника ADD' можно выразить как (1/2)xh, где h - высота треугольника ADD'.
Чтобы найти высоту, мы можем рассмотреть треугольник BDC. Так как отрезок CD равен отрезку AD, мы можем сказать, что треугольник BDC является равнобедренным треугольником.
Равнобедренный треугольник имеет равные высоту и основание, поэтому высота треугольника BDC также равна h.
4. Теперь, чтобы найти площадь треугольника BDC, мы можем использовать формулу для площади треугольника: (1/2)bh.
Основание треугольника BDC равно отрезку BC, то есть 2x, а высота равна h. Поэтому площадь треугольника BDC равна (1/2)(2x)(h) = xh.
5. Изначально было дано, что площадь треугольника ABC равна 1. Мы можем выразить площадь треугольника ABC через площадь треугольника BDC и треугольник ADD':
Площадь треугольника ABC = Площадь треугольника BDC + Площадь треугольника ADD'
1 = xh + (1/2)xh.
6. Теперь мы можем объединить уравнение и найти значения x и h:
1 = xh + (1/2)xh
1 = (3/2)xh
Разделим оба выражения на xh:
(1/xh) = 3/2
2 = 3/xh
Теперь найдем обратное значение от (3/xh):
(xh/3) = 1/2
Найдем значение произведения xh:
xh = 3/2
7. Возвращаемся к площади треугольника BDC, которая равна xh. Мы знаем, что xh = 3/2, так что площадь треугольника BDC равна 3/2.
8. Теперь мы должны найти площадь закрашенных фигур. Эти фигуры - это треугольники ACB и ADB'.
Объединяя эти две фигуры, мы получаем треугольник ADD', площадь которого мы уже нашли в предыдущем шаге.
Значит, площадь закрашенного треугольника ACB равно площади треугольника BDC, то есть 3/2.
Также площадь закрашенного треугольника ADB' равно площади треугольника ADD', которая также равна 3/2.
9. Итак, площади закрашенных фигур равны: треугольник ACB - 3/2 и треугольник ADB' - 3/2.