1. Алгебра
  2. Площадь прямоугольника с диагональю

Площадь прямоугольника с диагональю 6 см равна 9√3 см^2. найдите стороны прямоугольника

Sonechka20052005 Sonechka20052005    3   01.12.2021 00:02    1

Ответы
zlatashmyrova zlatashmyrova  10.01.2022 12:02

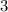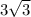ответ: высота - 3, ширина - 3\sqrt{3}.

Объяснение:

Формула площади прямоугольника через диагональ и любую сторону: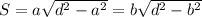 S = a\sqrt{d^2 - a^2} = b\sqrt{d^2 - b^2}.

Из условия известно: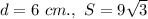 d=6\ cm.,\ S=9\sqrt{3}.

a\sqrt{36-a^2}=9\sqrt{3}\\a^2(36-a^2)=81*3\\36a^2-a^4=243\\36a^2-a^4-243=0\\-a^4+36a^2-243=0\\-t^2+36t-243=0\\t^2-36t+243=0\\D=(-36)^2-4*243=1296-972=324\\t_1=\frac{36-18}{2}=\frac{18}{2}=9\\t_2=\frac{36+18}{2}=\frac{54}{2}=27\\\\ a^2=9,\ \ \ \ \ \ \ \ \ \ a^2=27\\ a=\pm\ 3\ \ \ \ \ \ \ \ \ a=\pm\ 3\sqrt{3}\\a=-3\ \ \ \ \ \ \ \ \ \ a=-3\sqrt{3}\\a=3\ \ \ \ \ \ \ \ \ \ \ \ a=3\sqrt{3}\\

-3\sqrt{36-(-3)^2}=9\sqrt{3},\ -3\sqrt{36-9}=9\sqrt{3},\ -3\sqrt{27}=9\sqrt{3}\\-3\sqrt{3}\neq9\sqrt{3}\\

\\3\sqrt{36-3^2}=9\sqrt{3},\ 3\sqrt{36-9}=9\sqrt{3},\ 3\sqrt{27}=9\sqrt{3}\ 9\sqrt{3}=9\sqrt{3}\\9\sqrt{3}=9\sqrt{3}

-3\sqrt{3}\sqrt{36-(-3\sqrt{3})^2}=9\sqrt{3},\ -3\sqrt{3(36-(-3\sqrt{3})^2)}=9\sqrt{3},\ -3\sqrt{3(36-9*3)}=9\sqrt{3},\ -3\sqrt{3(36-27)}=9\sqrt{3},\ -3\sqrt{3*9}=9\sqrt{3},\ -3\sqrt{27}=9\sqrt{3},\ -9\sqrt{3}=9\sqrt{3}\\-9\sqrt{3}\neq9\sqrt{3}\\\\

3\sqrt{3}\sqrt{36-(3\sqrt{3})^2}=9\sqrt{3},\ 3\sqrt{3(36-(3\sqrt{3})^2)}=9\sqrt{3},\ 3\sqrt{3(36-9*3)}=9\sqrt{3},\ 3\sqrt{3(36-27)}=9\sqrt{3},\ 3\sqrt{3*9}=9\sqrt{3},\ 3\sqrt{27}=9\sqrt{3},\ 9\sqrt{3}=9\sqrt{3}\\9\sqrt{3}=9\sqrt{3}\\

a\neq-3\\a=3\\\\a\neq-3\sqrt{3}\\a=3\sqrt{3}\\\\a_1=3,\ a_2=3\sqrt{3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
RaritetnuWioN RaritetnuWioN  01.04.2020 19:30
ТЕСТ! 1. Якщо пряма є дотичною до кола, то вона має лише одну спільну точку з колом. так ні 2. Якщо пряма і коло мають одну спільну точку, то пряма є дотичною до...
marinka713 marinka713  01.04.2020 19:30
Найди следующие два члена арифметической прогрессии и сумму первых четырёх членов, если a1=4 и a2=−3,8. a3=? a4=? S4=?...
hshgahahah hshgahahah  01.04.2020 19:30
Тіло рухається прямолінійно зі швидкістю,яка змінюється за законом v(t)=2t+1(м/с).Знайдіть шлях,який пройшло тіло за третю секунду руху....
MadPrinter MadPrinter  01.04.2020 19:30
хотя бы что-нибудь из этого )1) 9cosx-13 sinx=1/sinx2) 1+9cos²x=11sinxcosx3) cosx+cos2x+cos3x+cos4x=04) 2(cos⁴x-sin⁴x)=15) cos6x=cos²2x-sin²2x6) cos3x+sin3x=cosx+sinx7)...
AbraevAidar AbraevAidar  01.04.2020 19:30
С АЛГЕБРОЙс решением и ответом​...
динозавр777 динозавр777  01.04.2020 19:30
Рационально решить неравенство...
бjulfyн бjulfyн  01.04.2020 19:30
Из какого сборника задания?...
МашаКан МашаКан  01.04.2020 19:30
Найдите первый член и знаменатель геометрической прогрессии, если б4-б1=-9, Б2+б3+б4=-6....
Ровног Ровног  01.04.2020 19:31
Сколько различных четырехзначных чисел можно записать с цифр 0,2,4,6 (без повторения)...
L1O2N3D4O5N L1O2N3D4O5N  01.04.2020 19:31
Найди значение выражения если b = -1/9...

Популярные вопросы