Площадь боковой поверхности правильной четырехугольной пирамиды равна 72 см^2, а площадь основания - 64 см^2. Найдите объем пирамиды.
Другие вопросы по теме Алгебра
Популярные вопросы
- ТЕСТ «Установление империи в Риме». 1 Народный трибун, выступивший...
1 - ҮЙ ТАПСЫРМАСЫ(9) Теңдеу құр және шығар.а) Арман бір сан ойлап,...
2 - Мартин Лютер ілімдерінен не түсіндің? ...
2 - -На какие этапы можно разделить образование мальчиков в древних...
1 - 7x^2-28=0 Решить записать корни через ; в порядке возрастания...
2 - Женя написал отзыв на свою любимую книгу , но забыл поставить...
3 - Прямо сейча! Нужно вставить неизвестное число в круг!...
2 - Rewrite these sentences. Use any or no. (Перефразируй предложения,...
1 - ответьте на во Для Н. Рубцова символ Родины-звезда,• для С. Есенина-...
3 - 5. Внутренние документы- 1. Первичные документы; 2. Накопительные...
1
V =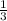 Sосн * h (1)
Sосн * h (1)
Sосн = 64 см²
Sб.п. = 72 см²
По сути, чтобы определить объём пирамиды, нужно узнать чему равна высота пирамиды.
Sб.п. = Pосн * h (2)
Pосн = 4a, где а - это сторона квадрата. Эту сторону можно найти из Sосн. Так как основание - квадрат (четырехугольная призма - правильная), то
Sосн = a², отсюда
a = √Sосн = √64 см² = 8 см
Pосн = 4*8 см = 32 см
(2) h = Sб.п./Pосн = 72см²/32см = 2,25 см
(1) V =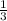 Sосн * h =
Sосн * h = 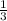 * 64 см² * 2,25 см = 48 см³
* 64 см² * 2,25 см = 48 см³
Надеюсь