1. Алгебра
  2. Площа повнОЇ поверхні циліндра

Площа повнОЇ поверхні циліндра
дорівнює 92п, а площа
його бічної поверхні -
56п.
Визначте площу
основи цього циліндра.
10

Dinozavrik2525 Dinozavrik2525    3   19.07.2022 01:26    1

Ответы
Vladarmani Vladarmani  19.07.2022 01:27

Объяснение:

Так як Sп.п. = Sб.п. + 2Sосн., то

2Sосн. = Sп.п. - Sб.п. = 92π - 56π = 36π.

Звідси отримаємо:

2Sосн. = 36π

Sосн. = 36π : 2

Sосн. = 18π

ПОКАЗАТЬ ОТВЕТЫ
Хєю Хєю  19.07.2022 01:27
ответ:

Площадь основания цилиндра равна 18π.

Объяснение:

ЗАДАНИЕ: площадь полной поверхности цилиндра равна 92π, а площадь его боковой поверхности - 56π. Определить площадь основания этого цилиндра.

Дано:

S = 92π

S_{b} = 56\pi

Найти:

S_{osn} - ?

Площадь полной поверхности цилиндра находится по формуле

\boxed {S =S_{b} + 2S_{osn}}, где

S - площадь полной поверхности цилиндра,
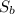S_{b} - площадь боковой поверхности цилиндра

S_{osn} - площадь основания цилиндра.

Выразим отсюда площадь основания цилиндра:

2S_{osn} = S - S_{b}

\boxed {S_{osn} = \frac{S - S_{b} }{2}}

Найдем площадь основания цилиндра:

S = \frac{92\pi - 56\pi }{2} = \frac{36\pi }{2} = 18\pi

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Хушкьвь Хушкьвь  20.08.2019 07:00
Найдите значение коэффициента а , если известно, что график квадратичной функции: y = ах2+4х+5, пересекает ось абсцисс в точке м(-10; 0) , подробно (если вам непонятно,...
sofia20015 sofia20015  20.08.2019 07:00
Найдите длину векторного произведения векторов j+k и i+k+j...
Inna050798 Inna050798  20.08.2019 07:00
Составь таблицу истинности для формулы (pvg)v(┐pv┐g)...
Gaky Gaky  08.06.2019 16:30
Найти значение выражения при х=-4 |х-3|-|2х+5|...
Adam123RUS Adam123RUS  08.06.2019 16:30
Решите систему уравнений (2х+3)^2=5y (3x+2)^2=5y...
cocles cocles  08.06.2019 16:30
Кто первый ввел переменную в ? ну x и y...
Maks23241 Maks23241  08.06.2019 16:30
Найдите все значения параметра р , при которых уравнение 2px2+(4р-3)х+2р-6=0 имеет корни...
larry19 larry19  08.06.2019 16:30
Выясните, имеет ли решение система и сколько: знак системы 5х-у=11 -10х+2у=-22...
nastya892968060 nastya892968060  08.06.2019 16:30
Вычислить площадь фигуры, ограниченную линиями: y=4-x^2, y=2-x...
bhgd bhgd  08.06.2019 16:30
Выражение числитель (х-5)*(х+1)+х^2-2х-3 знаменатель х-4 при х=7,31...

Популярные вопросы