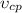Первые 180 км автомобиль ехал со скоростью 90 км/ч, следующие 200 км со скоростью 100 км/ч, а затем 160 км - со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Другие вопросы по теме Алгебра
Популярные вопросы
- Як можна назвать місто в якому живуть цифри? (для сказки)...
2 - Что значит глубоко нравственное произведение...
2 - Решите уравнения в столбик ! 0,3x+2,4x=270 0,2*(5x+x)=12 2x+x+0,6=4,2...
1 - Скласти програму (pascal abc)на знаходження мінімального числа в двохвимірном...
2 - Үшін, туралы, жайлы шылаулары қай септіктен кейін келетінің көрсетіңіз?...
1 - На фрагменті одного ланцюга днк нуклеотиди розташовані в послідовності,...
2 - Рассчитайте массовую долю в процентах хлорида кальция в растворе, полученном...
2 - Впервой бочке в 4 раза больше меда, чем во второй. если из первой бочки...
3 - Закончите уравнения возможных реакций, укажите для одной из этих реакций...
3 - №16 i. откройте скобки, употребив глагол в правильной временной форме....
3
99 км/ч
Объяснение:
Дано:
Найти: