Периметр прямоугольника равен 56 см. Какими должны быть размеры его сторон, чтобы площадь прямоугольника была наибольшей? Стороны прямоугольника должны быть
(?)см и (?) см
Максимально возможная площадь прямоугольника при данном периметре равна (?) см2.
Другие вопросы по теме Алгебра
Популярные вопросы
- 5 сынып адебиет «Анасын сашынган бала» окигасынын сюжеты Отиниш...
1 - 4 Complete the adjective with the correct ending (-ed or -ing)....
3 - Постройте график функции:...
3 - , чем сможете. Нужно до 11:00 выполнить. За каждое выполненное...
2 - написать эссе. Манаш Козыбаев. ЭССЕ на тему: Политическая работа...
2 - Places in a town. Lesson 1. Listen and choose either True or...
1 - 2. Продолжи словосочетания. Запиши в тетрадь.Где может находиться...
2 - ответь Януш Корчак— польский писатель, педагог, врач. Легенда...
2 - Заполни пропуски, выбрав верный вариант из выпадающего списка....
1 - What did the man with the scar look like? What was he like?...
2
14 см и 14 см
196 см**2
Объяснение:
наибольшая площадь при одинаковом периметре будет у квадрата
56/4= 14
ок. докажем
пусть у нас есть квадрат с стороной х. его периметр - 4х, а площадь -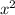
сделаем из квадрата прямоугольник того же периметра. его стороны будут (х-а) и (х+а)
периметр будет по-прежнему 4х, а площадь (х-а) * (х+а) =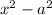
т е у любого прямоугольника того же периметра площадь будет меньше, чем у квадрата