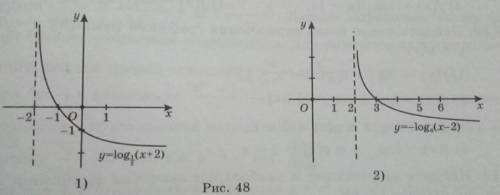
Перечислите свойства функции у= f (х) график которой изображен на рисунке 48

Объяснение:

1) Область Определения  Функции x ∈ (-2; +∞)

   Нули  = пересечение с осями (-1;0) и (0; -1)

    Убывает на всей ООФ

   Промежутки знакопостоянства y >0 при x ∈ (-2; -1), y <0 при x ∈ (-1; +∞)

     Ни четная, ни нечетная

   Непериодическая

Экстремумов нет, область значений (-∞; +∞)

Вертикальная асимптота х = -2

2) Область Определения  Функции x ∈ (2; +∞)

   Пересечение с ox (3;0)

    Убывает на всей ООФ

   Промежутки знакопостоянства y >0 при x ∈ (2; 3), y <0 при x ∈ (3; +∞)

     Ни четная, ни нечетная

   Непериодическая

Экстремумов нет, область значений (-∞; +∞)

Вертикальная асимптота х = 2

Добрый день! Рад помочь вам с этим вопросом.

На графике функции y = f(x), изображенном на рисунке 48, можно выделить несколько свойств функции:

1. Область определения: это множество значений аргумента x, для которых функция определена. По графику видно, что функция определена для всех значений x, начиная от минимального значения x на графике и до максимального значения x на графике. Таким образом, можно сказать, что область определения функции y = f(x) в этом случае - это отрезок [a, b], где a и b - минимальное и максимальное значения x на графике соответственно.

2. Область значений: это множество значений функции y, которые она может принимать. Смотря на график, видно, что все значения y на графике лежат в определенном диапазоне от некоторого минимального значения y_min до некоторого максимального значения y_max. Таким образом, можно сказать, что область значений функции y = f(x) в этом случае - это отрезок [y_min, y_max].

3. Монотонность: это свойство, указывающее на то, как меняется функция при изменении аргумента. На графике можно увидеть, что функция y = f(x) убывает (за исключением некоторых участков, где происходит возрастание) по мере увеличения аргумента x на интервалах [a, b], [c, d] и [e, f]. Это можно интерпретировать как то, что функция убывает на определенных промежутках и возрастает на других.

4. Точки экстремума: это точки, где график функции имеет максимум или минимум. На графике можно заметить, что есть точка, где график функции достигает минимального значения и одна точка, где он достигает максимального значения. Эти точки называются экстремумами функции и можно обозначить их как (x_min, y_min) и (x_max, y_max) соответственно.

5. Наличие асимптот: это прямые или кривые, которые график функции приближается по мере того, как аргумент стремится к бесконечности или как функция приближается к определенному значению. На графике можно заметить, что график функции имеет горизонтальную асимптоту, это может быть граница функции при стремлении аргумента x к бесконечности. Ее можно обозначить как y = k, где k - значение, которому приближается функция.

Это основные свойства, которые можно наблюдать на графике функции y = f(x) изображенном на рисунке 48. Надеюсь, это ответит на ваш вопрос. Если у вас есть еще вопросы, не стесняйтесь задавать!