Отметьте точки пересечения функции f x = -2x 2+x+3 с осями координат
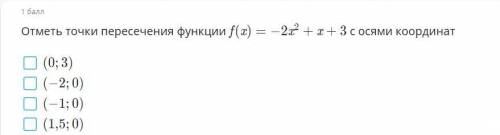
Другие вопросы по теме Алгебра
Популярные вопросы
- Хронологические рамки Раннего Возрождения: Выберите один ответ:...
1 - Создайте диалог со своим партнером по содержанию текста для прослушивания....
2 - Нужно заполнить таблицу как хлодвиг управлял государством...
3 - Самые элементарные вопросы по функции. И если кто сможет объясните...
3 - ЕВ 20. Прочитайте. Спишите, вставляя пропущенные буквы. Укажите...
3 - No3 Дано три числа a,B,C. a:8=2:3, a:c= 2:5, сума чисел віс дорівнює...
3 - Выбери правильные варианты нахождения среднего арифметического значения....
1 - Тема ,идея 148 сонета .шекспир...
3 - Можно стих написать русскими буквами не переводить а написать русскими...
3 - Задумайтесь Подумайте о причинах объединения людей в коллективы....
3
Для начала, давайте определим, с какими осями координат у нас будут пересечения. У нас есть две оси координат: ось абсцисс (горизонтальная ось) и ось ординат (вертикальная ось).
Точки пересечения с осью абсцисс имеют вид (x, 0), где x - это значение абсциссы. Точки пересечения с осью ординат имеют вид (0, y), где y - это значение ординаты.
Теперь давайте найдем точки пересечения с осью абсцисс. Для этого мы должны приравнять функцию f(x) к нулю и решить полученное уравнение:
-2x^2 + x + 3 = 0
Это уравнение квадратное. Мы можем решить его с помощью формулы дискриминанта:
D = b^2 - 4ac
D = 1^2 - 4*(-2)*(3)
D = 1 + 24
D = 25
Так как дискриминант положителен, это значит, что уравнение имеет два действительных корня.
Теперь найдем сами корни уравнения, используя формулу квадратного корня:
x = (-b +/- sqrt(D)) / (2a)
x1 = ( -1 + sqrt(25) ) / (-4)
x1 = ( -1 + 5) / (-4)
x1 = 4 / (-4)
x1 = -1
x2 = ( -1 - sqrt(25) ) / (-4)
x2 = ( -1 - 5) / (-4)
x2 = -6 / (-4)
x2 = 3/2
Теперь мы нашли значения абсцисс точек пересечения с осью абсцисс. Первая точка имеет координаты (-1, 0), а вторая точка имеет координаты (3/2, 0).
Теперь давайте найдем точку пересечения с осью ординат. Для этого мы должны подставить x = 0 в уравнение функции f(x):
f(0) = -2(0)^2 + (0) + 3
f(0) = 0 + 0 + 3
f(0) = 3
Получили, что точка пересечения с осью ординат имеет координаты (0, 3).
Итак, точки пересечения функции f(x) = -2x^2 + x + 3 с осями координат - это:
1) Точка (-1, 0), где функция пересекает ось абсцисс.
2) Точка (3/2, 0), где функция также пересекает ось абсцисс.
3) Точка (0, 3), где функция пересекает ось ординат.