Отличники ! ) ЗАДАНИЕ:
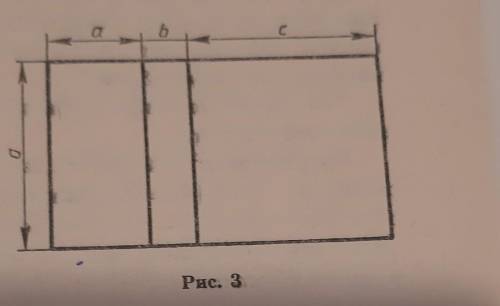
составьте два выражения для вычисления площади фигуры, изображенной на рисунке 3 (изобрж. на фото) докажите, что полученные выражения тождественно равны.
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание :составить инструкцию о правилах поведения пассажиров...
1 - Решите умадлддяю И не обращайте внимания на нижний текст 1....
2 - Поле образовано точечным зарядом q = 1,2*10 -7 Кл. Какую работу...
3 - Решите нормально Казахский Язык 6кл ( Прочитайте текст. ответьте...
1 - ответить на Вопросы 2,3,4(Заполнить таблицу) ...
3 - 1. Розгляньте парні й непарні плавці. Яке розташування й будову...
3 - 1) James Cook discovered Australia.2) People grow coffee in...
3 - Определить момент относительно точки А. Длина АВ=1м, угол ВАС=ВСА=750,...
2 - При взаимодействии водяных паров объемом 16,8 л (н.у) с раскаленным...
3 - 4) The pyramids (build) for the pharaohs.5) The light bulb(invent)...
3
Фигура, изображенная на рисунке, состоит из двух прямоугольников. Давайте дадим им названия, чтобы было проще обсуждать: пусть основной прямоугольник будем называть "А", а вспомогательный - "Б".
Теперь посмотрим на основной прямоугольник "А", который имеет длину 10 и ширину 8. Чтобы вычислить его площадь, нужно умножить длину на ширину. Таким образом, выражение для площади прямоугольника "А" будет: А = 10 * 8 = 80 (единиц площади).
Посмотрим теперь на вспомогательный прямоугольник "Б", который внутри основного. Он имеет длину 4 и ширину 6. Аналогично прошлому случаю, нужно умножить длину на ширину. Таким образом, выражение для площади прямоугольника "Б" будет: Б = 4 * 6 = 24 (единицы площади).
Теперь, чтобы доказать, что выражения тождественно равны, нужно сложить площади обоих прямоугольников и убедиться, что сумма равна площади всей фигуры.
Сумма площадей выражается так: А + Б = 80 + 24 = 104 (единицы площади).
Теперь давайте посмотрим на саму фигуру на рисунке. Видим, что ее площадь можно разложить на два прямоугольника: основной и вспомогательный. Если мы сложим их площади, то получим площадь всей фигуры. То есть, площадь фигуры также равна 104 (единицы площади).
Таким образом, мы видим, что полученные выражения для площади фигуры тождественно равны, так как оба дают одинаковое значение 104.
Надеюсь, это объяснение поможет вам понять решение задания. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их.