ОТ В уравнении 19 получается 2 решения:
х=-arctg4+пn
x=п/3+пn
Как понять, принадлежит ли какой-нибудь корень из первого решения (с арктангенсом) отрезку [п/3; 2п/3]
larisa114
2
11.08.2020 21:06
2 
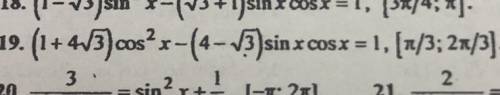
Популярные вопросы
- Почему вавилон торговым и ремесленным центром древнего востока? 20...
1 - На какие вопросы отвечает каждый второстепенный член?...
1 - Пословицы из слов от дело в руки скуки бери...
1 - В9-12 веках основную часть сельского населения древней руси составляли...
2 - Длина дна прямоугольного бассейн в 5 раз больше его ширины, причём...
3 - Краткое содержание по в ю драгунскому друг детства...
2 - На земле существует 250000 видов животных 4/5 всех видов состовляют...
2 - Мальчик с огромной коллекции жуков и пауков всего у них 8 голов и 54...
1 - Как решить эту . по железной дороге нужно перевезти 750 тонн зерна....
2 - Преобразуйте в многочлен стандартного вида: a) (х+7у)(х-7у) б) (m+5)^2-3m(m-4)...
1
Смотри рисунок.
Арктангенс 4 явно больше чем пи/3, потому что тангенс пи/3 это только корень из трех. Ну и как любой арктангенс, он меньше чем пи/2
Значит число "пи-arctg4" лежит между пи/2 и 2пи/3, и разумеется, принадлежит указанному отрезку.