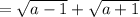Освободитесь от внешнего радикала в выражении, представив подкоренное выражение в виде квадрата

где 
Другие вопросы по теме Алгебра
Популярные вопросы
- Выполните деление. (на картинке)...
1 - Длина одного отрезка на 1 см больше второго и на 4 см больше третьего,могут...
3 - Творческое задание: создать в графическом редакторе Paint открытку (рисунок)...
1 - Чому відбувается закономірне зменшення кількості видів рослин і тварин від...
2 - Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно...
3 - Напишите небольшое ироничное сочинение к иллюстрации. (Примерно на листок тетради)...
2 - сделайте сор так что нужно сделать: (1)по содержанию текста сотавить 2 во определить...
2 - Замени развёрнутое описание одним словом с не-. Отсутствие веры — Немедленно,...
3 - Який момент в житті героїв був кульмінаційним твір фах...
1 - Скажите на милость сколько будет 2+2, а то я в 11 класс и незнаю. Кто получит...
3
Заметим, что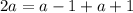 . Тогда
. Тогда 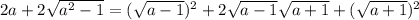 - преобразования делались с учетом того, что
- преобразования делались с учетом того, что 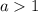 . Получаем
. Получаем 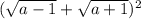 . Извлекая корень, получаем
. Извлекая корень, получаем 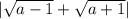 . С учетом положительности каждого корня:
. С учетом положительности каждого корня: