1. Алгебра
  2. Определите знаменатель бесконечно

Определите знаменатель бесконечно убывающей геометрической прогрессии, если сумма ее членов с нечетными номерами вдвое больше, чем сумма всех ее членов

mik42 mik42    3   09.07.2021 08:14    1

Ответы
вирона1 вирона1  09.07.2021 08:20

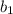Пусть b_1 - первый член данной прогрессии, а 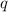q - ее знаменатель.

Тогда, сумма бесконечно убывающей геометрической прогрессии:

S=\dfrac{b_1}{1-q}

Рассмотрим члены этой прогрессии с нечетными номерами. Это также геометрическая прогрессия с первым членом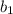 b_1 и знаменателем 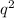q^2, причем геометрическая прогрессия бесконечно убывающая.

Сумма этой бесконечно убывающей геометрической прогрессии:

S=\dfrac{b_1}{1-q^2}

По условию эта сумма вдвое больше, чем предыдущая:

\dfrac{b_1}{1-q^2}=2\cdot\dfrac{b_1}{1-q}

\dfrac{b_1}{(1-q)(1+q)}=\dfrac{2b_1}{1-q}

b_1(1-q)=2b_1(1-q)(1+q)

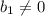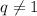Поскольку b_1\neq 0 и q\neq 1, то сократим:

1=2(1+q)

1+q=\dfrac{1}{2}

q=-\dfrac{1}{2}

ответ: -1/2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
mkagermazov mkagermazov  05.12.2021 20:15
Упростить выражение: (-3a^3y^4)^4...
irna200 irna200  05.12.2021 20:15
Знайдіть різницю многочленів: а) 4х3 + 3х2 + х – 4 і 2х3 – х2 + 2х + 7; б) –4m3 + 4m2 + m – 1 і –4m3 + 4m2 + m + 1;...
nastyakulikova5 nastyakulikova5  05.12.2021 20:14
Вот вам еще задачки по алгебре...
ПочтиОтличникМакс ПочтиОтличникМакс  05.12.2021 20:13
У(у-6)-(у-11)²=у-1 5х(х-3)-5(х-2)²=15 решите уравнения...
ladakorobova ladakorobova  05.12.2021 20:13
3. Составьте из данных уравнений систему, имеющую решением пару: 1) (3:0) 2) (2;-3)...
Istominyura Istominyura  05.12.2021 20:12
1.Найди корни квадратного уравнения x2+5x+6=0 (первым вводи больший корень; если корни одинаковые, впиши одинаковые числа в оба окошка). x1 = x2 = 2.Не используя формулу корней,...
Neznayka322 Neznayka322  05.12.2021 20:09
Розв яжіть графічно -x+3x-6=√x ів...
nadyushasukhan nadyushasukhan  10.11.2021 03:55
Упростите выражение: а) 7х - 3у + 3х - 6у; б) 8(4а-6) - 3; в) 9х – (х - 8) + (2 х - 1)....
Nastja2196 Nastja2196  10.11.2021 06:00
6 (у-4)-3(y+8)=-2 (y-1)это уравнение...
Alllexxxsss Alllexxxsss  10.11.2021 06:37
Обчисліть значення виразу 4x²у- ху² - 3x²y+ ху² - xy +6, якщо x=-3, у = 2....

Популярные вопросы