Определите значения a, при которых уравнение 4x^3+4x^2+ax=0 имеет два корня. найдите эти корни

Произведение равно нулю в том случае, когда хотя бы один из множителей равен нулю

Один корень уже известен. Теперь нужно найти те значения параметра а, при котором квадратное уравнение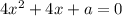 имеет один действительный корень.

Квадратное уравнение имеет один корень, если его дискриминант равен нулю, т.е.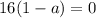 откуда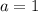

ответ: a = 1.