Определите, при каких значениях параметра a имеет единственное решение уравнение: (x+a)/(x-1)+(a-3x)/(x+3)=2

Ответы

живууууу 15.10.2020 15:29

$\frac{x+a}{x-1}+\frac{a-3x}{x+3}=2$

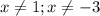
ОДЗ: $x\neq 1; x\neq -3$

Перенесем 2 в левую часть и преобразуем:

$\frac{x+a}{x-1}+\frac{a-3x}{x+3}-2=0;\\\\\frac{(x+a)(x+3)+(a-3x)(x-1)-2(x-1)(x+3)}{(x-1)(x+3)}=0;\\\\\frac{x^2+3x+ax+3a+ax-a-3x^2+3x-2x^2-4x+6}{(x-1)(x+3)}=0;\\\\-4x^2+2ax+2x+2a+6=0;|:(-2)\\\\2x^2-ax-x-a-3=0;\\\\2x^2-(a+1)x-a-3=0. (*)$

Ищем дискриминант, так как уравнение априори квадратное:

$D=(a+1)^2-4\cdot2\cdot(-a-3)=a^2+2a+1+8a+24=a^2+10a+25=(a+5)^2.$

Исходное уравнение имеет единственное решение в двух случаях.

1) уравнение (*) имеет одно решение (D=0), которое удовлетворяет ОДЗ. Дискриминант равен 0 при a = -5. Тогда корень уравнения равен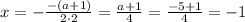 $x=-\frac{-(a+1)}{2\cdot2}=\frac{a+1}{4}=\frac{-5+1}{4}=-1$ . Он удовлетворяет ОДЗ, поэтому a = -5 точно пойдет в ответ.

2) уравнение (*) имеет два решения(D>0), но один из корней отпадает по ОДЗ.

Дискриминант положителен при a ≠ -5. Тогда корни уравнения равны

$x=\frac{-(-(a+1))\pm\sqrt{(a+5)^2}}{2\cdot2}=\frac{a+1\pm(a+5)}{4};\\\\ x_1=\frac{a+1+a+5}{4}=\frac{2a+6}{4}=\frac{a+3}{2};\\\\ x_2=\frac{a+1-a-5}{4}=\frac{-4}{4}=-1$

Один из корней - x = -1 - удовлетворяет ОДЗ при любом значении параметра, поэтому корень x = (a+3)/2 должен наоборот не удовлетворять, чтобы решение было ровно одно.

Проверим, при каких a корень x = (a+3)/2 совпадает с числами 1 или -3:

$\frac{a+3}{2}=1\Rightarrow a+3=2\Rightarrow a=-1; \\\ \frac{a+3}{2}=-3 \Rightarrow a+3 = -6\Rightarrow a=-9.$