Определите при каких значениях a оба корня уравнения равны нулю x^2-(a^2+3a)x+3[a]-a^2=0

Раз оба корня равны нули, значит они равные. А равные корни могут быть только при дискриминанте D=0.

D=b^2-4ac          a=1,b=-a^2-3a,c=3a-a^2    D=0

(-a^2-3a)^2-4(3a-a^2)=0

(a^2+3a)^2-4(3a-a^2)=0

Так и оставляем дискиминант.

x1=(-b-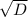)/2a.

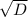x2=(-b+)/2a.

x1=x2=0, D=0

-b/2a=0

-(-a^2-3a)/2=0

a^2+3a=0

a(a+3)=0

a=0 или a=-3.

Теперь проверяем, удолетворяет ли найденные нами a решению уравнения с параметром. Для этого подставим их в уравнение дискриминанта:

(a^2+3a)^2-4(3a-a^2)=0

(0+0)^2-4(0-0)=0

0=0

a=0 - удолетворяет

(9-9)^2-4(-9-9)=0

72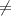0

a=-3 - не удолетворяет условию.

ответ: 0.