Определите квадратные уравнения из приведенных уравнений. Преобразуйте незаданные уравнения и запишите их в данное уравнение. A) 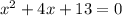
B) 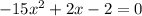
C) 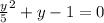
D) 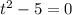
Другие вопросы по теме Алгебра
Популярные вопросы
- Разгадайте ребус,в котром одинаковые цифры обозначены одинаковыми буквами,а...
2 - Проверочное слово на ы в слове страницы...
1 - Какой из материков пресекают оба тропика? а) австралия б) южная америка,...
3 - Проспрягайте следующие глаголы в утвердительной, отрицательной и вопросительной...
3 - Найти пятую число не четное, чтоб получить ответ 30 вот пример 1+1+3+5+***=30...
1 - Составить слова существительные с окончаниями ло ло ло ло но ро...
2 - На сколько секунд: а) минута больше секунды; б) час больше минуты;...
1 - 15 л яблочно сока разлили в 5 банок поповну.сколько нужно таких банок...
3 - Перевод текста reaперевод текста read barbara s letter and say whatd...
3 - Вкаком предложении допущена ошибка при образовании падежной формы имени...
3
A) В данном уравнении у нас уже есть квадратный член, который является x в степени 2. Вторым членом является 4x, и третьим членом является 13. Чтобы определить квадратное уравнение, следует внимательно посмотреть на коэффициент при x в степени 2 — он равен 1. У нас есть число 1, умноженное на x в степени 2. Поэтому данное уравнение является квадратным уравнением.
B) В этом уравнении также присутствует квадратный член — это -15x в степени 2. Вторым членом является 2x, и третьим членом является -2. Коэффициент при x в степени 2 равен -15, поэтому и это уравнение является квадратным уравнением.
C) В данном уравнении у нас есть квадратный член, но он не записан явно. Мы видим уравнение
D) В данном случае есть квадратный член — это t в степени 2. Вторым членом является -5. Так как у нас есть только t в степени 2 и константа, то это также квадратное уравнение.
Определение квадратного уравнения основывается на наличии квадратного члена (буква в степени 2) в уравнении. Если такой член есть, то уравнение является квадратным.
Надеюсь, эта информация помогла тебе разобраться с задачей! Если у тебя остались вопросы, не стесняйся задавать их.