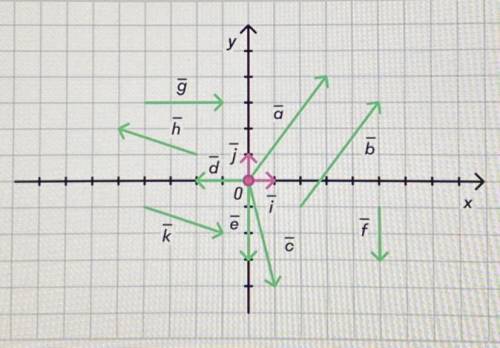
Определить координаты всех векторов

Для определения координат векторов на данной рисунке нам понадобятся две системы координат: сначала рассмотрим сетку из вертикальных и горизонтальных линий, а затем введём ортогональные оси XOY.

Давайте начнем с вектора AB. Мы можем представить его как вектор, образованный разностью координат концевой точки B и начальной точки A. Изображение показывает, что конечная точка B имеет координаты (1, 3), а начальная точка A - координаты (0, 0).

Используя формулу разности, мы можем вычислить координаты вектора AB:

AB = (x2 - x1, y2 - y1)
= (1 - 0, 3 - 0)
= (1, 3)

Таким образом, координаты вектора AB равны (1, 3).

Теперь рассмотрим вектор BC. По аналогии с предыдущим шагом, вектор BC можно выразить через координаты его концевой точки C (2, 1) и начальной точки B (1, 3):

BC = (x2 - x1, y2 - y1)
= (2 - 1, 1 - 3)
= (1, -2)

Координаты вектора BC равны (1, -2).

Аналогично, мы можем определить координаты вектора CD, используя конечную точку D (3, -1) и начальную точку C (2, 1):

CD = (x2 - x1, y2 - y1)
= (3 - 2, -1 - 1)
= (1, -2)

Координаты вектора CD также равны (1, -2).

Наконец, рассмотрим вектор DE, используя конечную точку E (4, -3) и начальную точку D (3, -1):

DE = (x2 - x1, y2 - y1)
= (4 - 3, -3 - (-1))
= (1, -2)

Координаты вектора DE также равны (1, -2).

Таким образом, координаты всех векторов изображенных на рисунке равны:

AB = (1, 3)
BC = (1, -2)
CD = (1, -2)
DE = (1, -2)