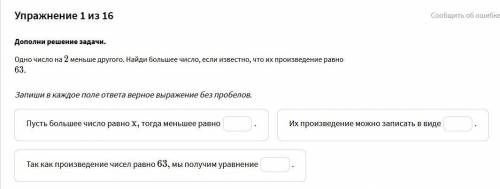
Одно число на 2 меньше другого. Найди большее число, если известно, что их произведение равно 63.

ответ: 9

Объяснение:

Смотри

Давайте решим эту задачу вместе!

В задаче сказано, что одно число на 2 меньше другого. Давайте обозначим эти числа как "x" и "x-2". Здесь "x" будет представлять большее число, поскольку "x-2" означает, что одно число (x) на 2 меньше другого числа.

Теперь вам известно, что произведение этих чисел равно 63. Это значит, что (x)(x-2)=63.

Чтобы решить это уравнение, мы можем установить его равным нулю и использовать метод факторизации. Для этого нам нужно перенести все выражения на одну сторону уравнения:

x^2 - 2x = 63

Теперь приведем уравнение в стандартную форму квадратного трехчлена:

x^2 - 2x - 63 = 0

Чтобы решить это уравнение, нам нужно факторизировать его или использовать квадратное уравнение. В данном случае легче воспользоваться факторизацией:

(x - 9)(x + 7) = 0

Здесь мы нашли два множителя, которые, умноженные вместе, дают нам ноль.

Из этого равенства следует, что x - 9 = 0 или x + 7 = 0. Решим каждое из уравнений по отдельности:

1) x - 9 = 0
x = 9

2) x + 7 = 0
x = -7

Теперь у нас есть два возможных значения для x: 9 и -7. Но у нас было изначальное условие, что одно число на 2 меньше другого. Это означает, что x должно быть больше, чем x-2. Если x = 9, то 9-2=7 и оно не соответствует нашему условию. Таким образом, мы можем отбросить это значение.

Поэтому, большее число, которое мы ищем, равно x = -7.

Итак, ответ на эту задачу: большее число равно -7.