Один из корней уравнения x²+10x+q=0 равен (-12). Найти другой корень и q
Другие вопросы по теме Алгебра
Популярные вопросы
- Был ли в россии парламент или совет? в 15-16 веке?...
2 - 1. Рассчитайте стандартную энтальпию реакции Fe3O4(к)+H2(г)→FeO(к)+H2O(г)....
1 - 3-тапсырма. Кез-келген етістікті ауыспалы өткен шақ және бұрынғы өткен шақта...
2 - Люди добрые . не можем сделать....
3 - 1)вычислите значение выражения ,b- 3 11 2) Вычислите значение выражения при...
1 - Більша основа рівнобічної трапеції дорівнює 10 см, бічна сторона 6 см. Гострий...
2 - 4. В Монетке рядом с домом мамин любимый торт стоит 360 рублей, ав Магните,...
1 - Из приведённых ниже тел выбери и отметь те, колебания которых будут свободными:...
3 - расправа над арабами и евреями обернулась страшным бедствием для страны. Подтвердите...
1 - 1. Парафин, содержащийся в свече, является источником огня. Если накрыть парафиновую...
3
Объяснение:
ответ: x₂=2 q=-24.
x1=-12, тогда 144-120+q=0? значит q=-24, если q=-24, то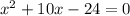 , значит x2=2
, значит x2=2
Объяснение:
D=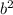 -4ac
-4ac
D=100+96=196
x=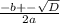
x2=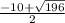 =2
=2
x1=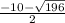 =-12
=-12