Очень Решите, это три номера. Заранее

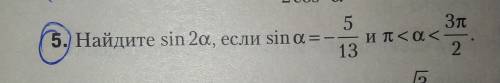
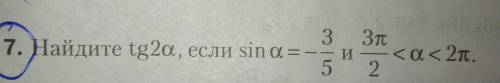
Другие вопросы по теме Алгебра
Популярные вопросы
- Прокоментуйте назву повісті н.бічуї шпага славка беркути...
3 - Уякий із зазначених часів (періодів) січова (військова) рада...
1 - Числа 0 і 1 написані в кожній клітинці таблиці розміром 5*5 що...
3 - Ад=дс, ао=ос. докажите что тр. авд=свд...
2 - Летим над островами карибского моря,краткое содержание.заранее...
2 - Життевий та творчий шлях ліни костенко. цитатней план...
3 - Масса угля в железнодорожном вагоне 60 тонн. самосвал может взять...
2 - Сочинение описание про кобрин на языке...
3 - Художественные средства(эпитеты, метафоры, риторические вопросы...
1 - Составте эссе 6-7 предложенный на тему насилие рождает насилие...
3
8.
n принадлежит Z.
5.
угол принадлежит 3 четверти => косинус отрицательный.
7.
угол принадлежит 4 четверти => косинус положительный.