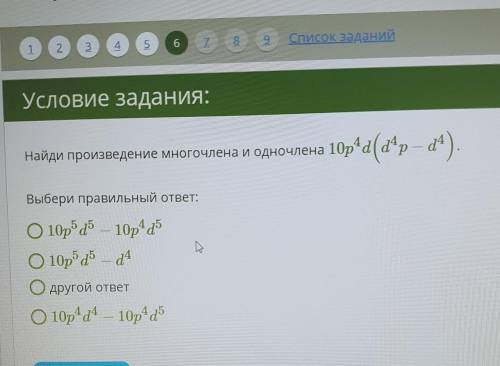
ОЧЕНЬ НУЖНО НЕ СДЕЛАЮ ДВА ПОСТАВЯТ найди произведение многочлена и одночлена 10p<4d(d<4p - d<4).
Выбери правильный ответ:

-10pd5 – 10p1a5
-10р d5 - d4
-другой ответ
-10p4 d4 - 10p4 d5​

Для решения этой задачи посмотрим на выражение, которое нужно умножить: 10p < 4d(d < 4p - d < 4).

Внутри скобок есть два множителя: d и (d < 4p - d < 4). Давайте рассмотрим каждый множитель по отдельности.

1. Умножение многочлена на одночлен:
10p умножаем на d. Для этого нужно перемножить коэффициенты и сложить показатели степеней. В итоге получим 10pd.

2. Умножение одночлена на одночлен:
d умножаем на (d < 4p - d < 4). Здесь также нужно перемножить коэффициенты и сложить показатели степеней. Важно обратить внимание на знак минус перед вторым одночленом в скобках. При умножении на отрицательное число меняется знак. Поэтому получим -d^2(4p - d < 4).

Теперь объединим оба выражения:
10pd - d^2(4p - d < 4).

Таким образом, правильный ответ на задачу будет: -10pd + d^2(4p - d < 4).