Очень нужна определить производные , пользуясь формулами дифференцирования.
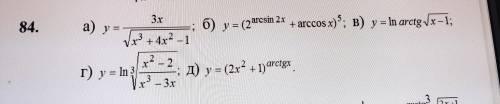
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто автор произведения каркаралы и акшолпан...
1 - Кто совершил первое кругосветное путешествие...
3 - Написать мини сочинение на тему : в гостях у земледельца .кто тому 24 пункта...
3 - Написать сочинение на тему почему фашистам удалось так легко прийти к власти...
1 - 4ч40 мин.+52мин вычислить столбиком...
2 - Придумать знаки символы которые озночали бы различные науки- , , биология...
1 - 90412-128*84: (6040-5848)*370+53878*0= решите действиями !...
3 - Научите как считать проценты было 2800 стало1653 на сколько процентов убавились...
1 - Рак из спичек ползёт в низ надо переложить 3 спички чтобы он полз в низ...
2 - 1) 3 5/14 * 7/9 - 2 3/14 * 7/9 2) 7 1/5 * 2 1/8+7 1/5 * 1/58 3) 3/4 * 1...
3
а)
б)
в)
г)
д)
формула: