ОЧЕНЬ НАДО КТО-НИБУДЬ(Нужно освободиться от иррациональности в знаменатели)
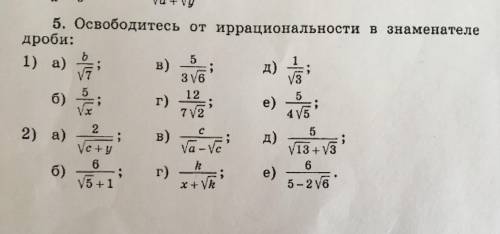
Другие вопросы по теме Алгебра
Популярные вопросы
- 7класс решить вырожение и найдите его значение-4(2,5а -1,5) + 5,5а - 8,...
1 - Вопросительные предложения со словами ружье листья муравьи подъем несъедобный...
3 - Все персонажи сказки мальчик звезда ....
1 - Как творчество баха, бетховена и моцарта повлияло на культуру эпохи просвещения?...
2 - Подберите проверочное слово и найдите кореь в словах скорлубка безрукавка...
2 - ответить what is your opinion the most important thing in your future profession...
2 - Задайте мне 10 вопросов по фильму одинокий рейнджер !...
3 - Найдите площадь квадрата, если его сторона равна 20см...
1 - Вкоком словосачетаний верно определён падеж имени прилагательного? 1) о...
2 - 1.верны ли суждения. ( да, нет) а) средневековые люди много путешествовали,...
3
В решении.
Объяснение:
1.
а) b/√7 * √7/√7 = b√7/7;
б) 5/√x *√x/√x = 5√x/x;
в) 5/3√6 *√6/√6 = 5√6/3*6 = 5√6/18;
г) 12/7√2 *√2/√2 = 12√2/7*2 = 12√2/14 = 6√2/7;
д) 1/√3 * √3/√3 = √3/3;
е) 5/4√5 * √5/√5 = 5√5/4*5 = 5√5/20 = √5/4.
2.
а) 2/(√c+y) * (√c+y)/(√c+y) = 2(√c+y)/(c+y);
б) 6/(√5 + 1) * (√5 - 1)/(√5 - 1) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 6(√5 - 1)/(√5)² - 1² =
= 6(√5 - 1)/(5 - 1) =
= 6(√5 - 1)/4 =
= 3(√5 - 1)/2;
в) с/(√a - √c) * (√a + √c)/(√a + √c) =
в знаменателе развёрнутая разность квадратов, свернуть:
= c(√a + √c)/(√a)² - (√c)² =
= c(√a + √c)/(a - c);
г) k/(x + √k) * (x - √k)/(x - √k) =
в знаменателе развёрнутая разность квадратов, свернуть:
= k(x - √k)/(x² - (√k)²) =
= k(x - √k)/(x² - k);
д) 5/(√13 + √3) * (√13 - √3)/(√13 - √3) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 5(√13 - √3)/(√13)² - (√3)² =
= 5(√13 - √3)/(13 - 3) =
= 5(√13 - √3)/10 =
= (√13 - √3)/2;
е) 6/(5 - 2√6) * (5 + 2√6)/(5 + 2√6) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 6(5 + 2√6)/(5² - (2√6)²) =
= 6(5 + 2√6)/(25 - 4*6) =
= 6(5 + 2√6)/1 =
= 6(5 + 2√6).